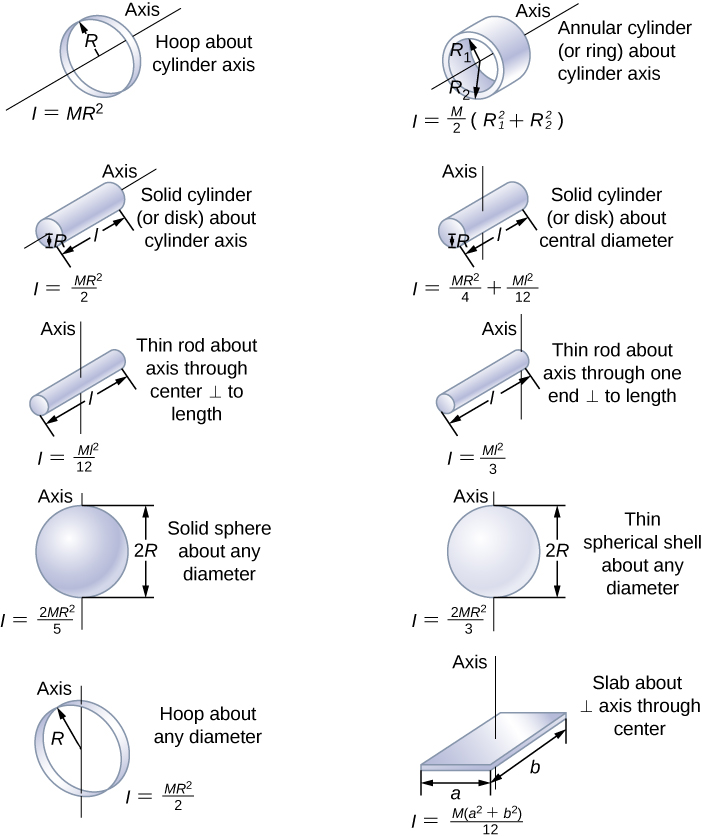
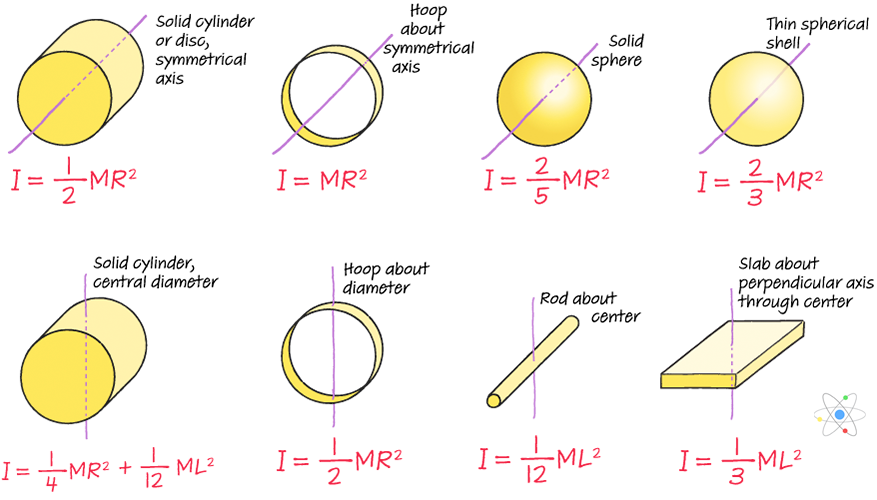
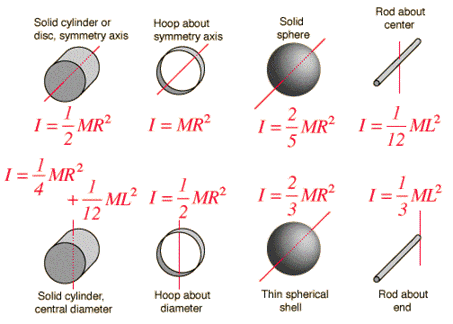
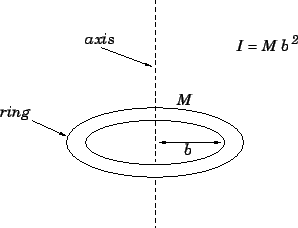
Moment of Inertia of a Thin Hoop
Calculating Moment of Inertia Point-objects small size compared to radius of motion. The formula of finding moment of inertia is.

Artificial Gravity Atomic Rockets Rocket Atom Gravity
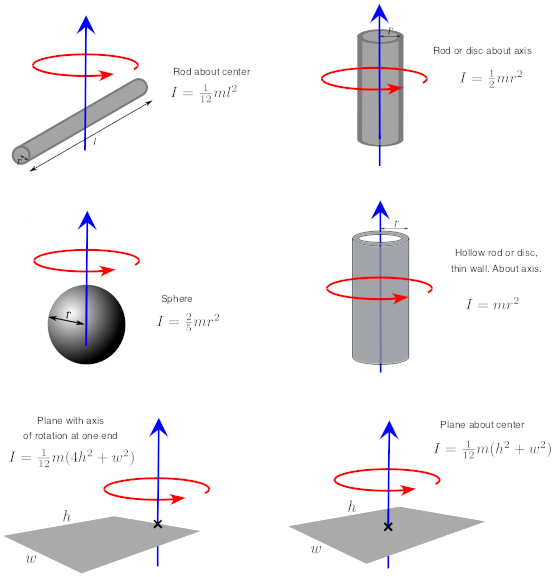
Disk Imagine rolling a hoop and a disk of equal mass.

. The distance from the differential mass dm is Rsinθ. The moment of inertia of a hollow circular cylinder of. Moment of inertia is proportional to an objects mass and to its distance from the rotational axis squared.
I 25 MR2 Hollow sphere through center. How do I modify my region R in order to take into account the uniform thin hoop that has no width. The hoop can also rotate around an axis that intersects the midpoint of the line from A to B and does not intersect the hoop as shown by the orange arrow.
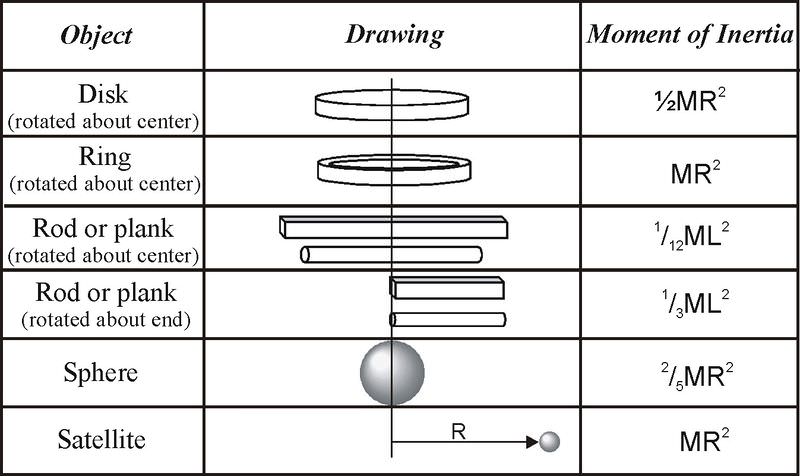
First we will look at a ring about its axis passing through the centre. I MR2 See textbook for more examples pg. I 12 MR2 Hoop through center.
Moment of inertia of a hoop about diameter will be l ½ MR². Dm M A dA 2 2 d m M A d A. The density is ρ M 2πRt.
Moment of inertia of a solid cylinder about central diameter will be I ¼ MR² 112 ML². Is there a way I could evaluate a hoop of width texDelta Rtex and find moment of inertia in terms of texDelta Rtex then let find the limiting value as texDelta Rtex. This may be compared with a solid cylinder of equal mass where Isolid kg m 2 or with a thin hoop or thin-walled cylinder where Ithin kg m 2.
Find the moment of inertia of a hoop a thin-walled hollow ring with mass M and radius R about an axis perpendicular to the hoops plane at an edge. I M r 2. Moment of Inertia Derivation - Hoop or Thin Cylindrical Shell.
Find the moment of inertia of a hoop a thin-walled hollow ring with mass M and radius R about an axis perpendicular to the hoops plane at an edge. I M r2 Moment of inertia for a thin circular hoop. Express your answer in units of kgm2.
The hoop can rotate around an axis that intersects the hoop at the points A and B as shown by the blue arrow in the diagram. Moment of inertia tells you how difficult it is to rotate an object. However we know how to integrate over space not over mass.
The radius of the hoop is R. It is equivalent to the mass in linear problems. I x I y m r 2 2 and the sum is I z I x I y.
We will derive the moment of inertia of a ring for both instances below. I 23 MR2 Solid disk through center. You could combine a bunch of hoops together to create a cylinder.
The distance from the rotational axis dominates over the objects mass due to the square power. Why does a thin cylindrical shell has the same moment of inertia of a hoop. Finding the Moment of Inertia of a Uniform Hoop with mass M and radius R rotating about its diameter hoops and rings are infinitely thin.
Why does a thin circular hoop of radius r and mass m have the following moments of inertia. Sample Questions based on Moment of inertia. Viewed from Beside the Axis.
Because the cross section of a cylinder is the same as a hoop. Jaylalemieu8826 is waiting for. We will assume the mass of the ring to be M and radius be R.
I r 2 d m where d m ρ d V 2 r π ρ. Find the moment of inertia of a hoop a thin-walled hollow ring with mass m and radius r about an axis perpendicular to the hoops plane at an edge. We define dm to be a small element of mass making up the rod.
We will further look at how the equations are derived. Apply Eq919 the parallel-axis theorem. Solid Cylinder or Thin Disk about Axis Through the Face.
The moment of inertia I kg m 2. Hollow Cylinder or Hoop. Thin Disk about Axis Through the Edge.
A thin hoop has a radius of 125 m and a mass of 750 g. I x I y mR 2 2. Yes I changed websites.
Find the moment of inertia of a hoop a thin-walled hollow ring with mass M 1kg and radius R 1m about an axis perpendicular to the hoops plane at an edge. The moment of inertia is I kg m 2 For a thin hoop about a diameter in the plane of the hoop the application of the perpendicular axis theorem gives Ithin hoop about diameter kg m 2 Show effect of hoop thickness. How to obtain I x I y m r 2 2 from here onwards.
Rectangular Plates Thin Rods and Boards Description. However the region is a hoop whose width is infinitely thin. Now we need to cut an elemental ring dx at the.
Express your answer in terms of the variables m and r. Viewed Along the Axis. I Σm ir i 2 Solid sphere through center.
The distribution of mass versus radius stays the same only the amount of mass varies the m in m r2. Find step-by-step Physics solutions and your answer to the following textbook question. The center of mass of the hoop is at its geometrical center.
As the axis is across the diameter. 919 2 2 2 I MR d R I MR cm and so 2. Label a diffcrcntial clement on the diagram along with its differential length di note.
11 rows Calculate the moment of inertia of the remaining disc about an axis perpendicular to the plane of. Hence dI r2dm 1 1 d I r 2 d m. Figure 1025 Calculation of the moment of inertia I for a uniform thin rod about an axis through the center of the rod.
In order to continue we will need to find an expression for dm d m in Equation 1. The volume is 2πRt. Moment of inertia for a thin circular hoop.
The thickness is t. Moment of inertia of a thin spherical shell will be I 23 MR² Moment of inertia of a rod about its end will be I 13 ML². The moment of inertia is.
The moment of inertia integral is an integral over the mass distribution.

Uniform Thin Hoop Rotational Inertia Derivation Youtube
10 4 Moment Of Inertia And Rotational Kinetic Energy University Physics Volume 1

Rotational Inertia Greg School

Pin By Daniel Armstrong On Edutaning Html Book In This Moment Rod
Rotational Inertia Article Khan Academy

Moment Of Inertia Images Stock Photos Vectors Shutterstock

Deriving The Moment Of Inertia For A Hoop Ring And Disk Youtube

Moments Of Inertia Physics And Mathematics Physics Engineering Science
Homework And Exercises How To Derive The Moment Of Inertia Of A Thin Hoop About Its Central Diameter Physics Stack Exchange
Moment Of Inertia Read Physics Ck 12 Foundation

Mass Moment Of Inertia Equations Have An Equation Table Physics Lessons Inertia Mathematics Geometry
Comparing Moments Of Inertia For Common Objects W Diagrams
Moment Of Inertia Calculation Formula The Constructor

Finding The Moment Of Inertia From A Point To A Ring To A Disk To A Sphere By Rhett Allain Medium

The Moment Of Inertia Of A Hoop Youtube

Moment Of Inertia Derivation Hoop Or Thin Cylindrical Shell Youtube
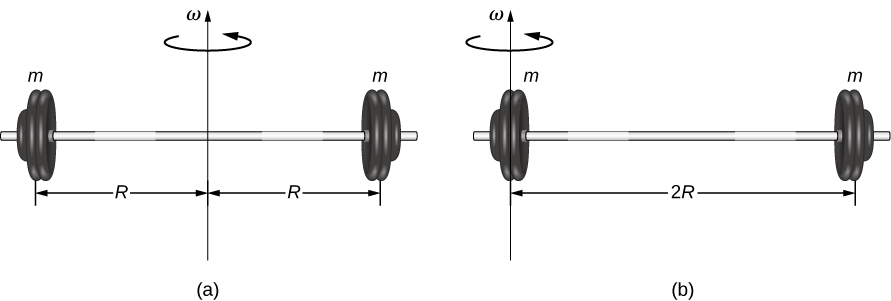
10 5 Calculating Moments Of Inertia University Physics Volume 1
Comments
Post a Comment